Today, I want to explain a bit about how to solve one of the simplest and fundamental equations in PDE.
Poisson Equation
\begin{aligned} -\nabla \cdot (q(u)\nabla u) = f \end{aligned}
Here, the coefficient $q(u)$ makes the equation nonlinear.
Applying the identity $\nabla \cdot (uv) = (\nabla u)v + u\cdot \nabla v$
\begin{aligned} -\int_{\Omega} (\nabla \cdot (q(u)\nabla u)) v\,\mathrm{d}x &= \int_{\Omega} (q(u)\nabla u) \cdot \nabla v \, \mathrm{d} x - \int_{\Omega} \nabla\cdot (q(u)\nabla u) v \,\mathrm{d}x\cr &= \int_{\Omega} f v\,\mathrm{d}x\cr \text{Divergence theorem:} &\cr &= \int_{\Omega} (q(u)\nabla u) \cdot \nabla v \, \mathrm{d} x - \int_{\partial \Omega} \mathrm{n}\cdot (q(u)\nabla u) v \,\mathrm{d}s \end{aligned}
Applying weak form transformation: $\forall v \in \partial\Omega: v = 0$
\begin{aligned} &\int_{\Omega} (q(u)\nabla u) \cdot \nabla v \,\mathrm{d}x = \int_{\Omega} f v\,\mathrm{d}x\cr F(u, v) &= \int_{\Omega} (q(u)\nabla u \cdot \nabla v - fv)\,\mathrm{d}x \end{aligned}
Now, for the variational form:
\begin{aligned} a(u,v) &= L(v)\cr &= \int_{\Omega} (q(u)\nabla u) \cdot \nabla v \,\mathrm{d}x \end{aligned}
and $L(u,v) = \int_{\Omega} f v\,\mathrm{d}x$
V = FunctionSpace(mesh, 'P', 1)
u_D = Expression(u_ccode, degree=2)
bc = DirichletBC(V, u_D, boundary)
u = Function(V)
v = TestFunction(V)
f = Expression(f_ccode, degree=1)
F = q(u)*dot(grad(u), grad(v))*dx - f*v*dx
solve(F == 0, u, bc)
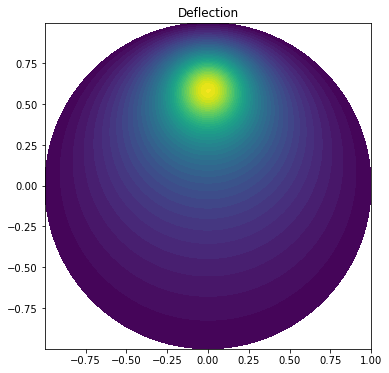
Membrane Poisson Equation
We want to compute the deflection $D(x,y)$ of a two-dimensional, circular membrane of radius $R$, subject to a load $p$ over the membrane. The appropriate PDE model is:
\begin{aligned} -T\nabla^{2}D = p \quad \text{in}\; \Omega = \lbrace (x,y) \big\vert x^{2}+y^{2} \leq R \rbrace \end{aligned}
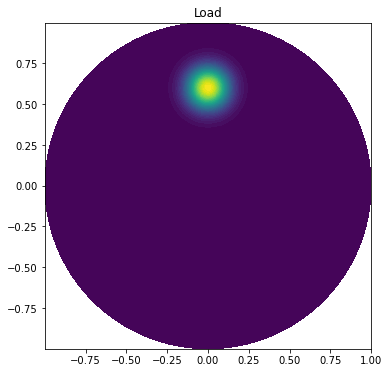
Here, $T$ is the tension in the membrane (constant), and $p$ is the external pressure load. The bounday of the membrane has no deflection, implying $D = 0$ as a boundary condition. A localized load can be modeled as a Gaussian function:
\begin{aligned} p(x,y) = \frac{A}{2\pi\sigma} \exp\bigg( -\frac{1}{2}\Big(\frac{x-x_{0}}{\sigma}\Big)^{2} - \frac{1}{2} \Big(\frac{y-y_{0}}{\sigma}\Big)^{2} \bigg) \end{aligned}
The parameter $A$ is the amplitude of the pressure, $(x_{0}, y_{0})$ the localization of the maximum point of the load, and $\sigma$ the “width” of $p$. We will take the center $(x_{0}, y_{0})$ of the pressure to be $(0, R_{0})$ for some $0<R_{0}<R$.
\begin{aligned} \nabla^{2} w = 4 \exp \big( -\beta^{2}(x^{2} + (y-R_{0})^{2}) \big), \quad (x,y) \in \Omega \end{aligned}
Applying the identity $\nabla \cdot (uv) = (\nabla u)v + u \cdot \nabla v$:
\begin{aligned} -\int_{\Omega} (\nabla^{2} w) v\,\mathrm{d}x &= \int_{\Omega} \nabla w \cdot \nabla v \, \mathrm{d} x - \int_{\Omega} \nabla\cdot (\nabla w) v \,\mathrm{d}x\cr &= \int_{\Omega} 4\exp(-\beta^{2}(x^{2}+(y-R_{0})^{2})) v\,\mathrm{d}x\cr \text{Divergence theorem:}& \cr &= \int_{\Omega} \nabla w \cdot \nabla v \, \mathrm{d} x - \int_{\partial \Omega} \mathrm{n}\cdot (\nabla w) v \,\mathrm{d}s \end{aligned}
Applying weak form transformation $\forall v \in \partial\Omega, v = 0$:
\begin{aligned} \int_{\Omega} \nabla w \cdot \nabla v \,\mathrm{d}x = \int_{\Omega} 4\exp(-\beta^{2}(x^{2}+(y-R_{0})^{2})) v\,\mathrm{d}x \end{aligned}
Now, for the variational form:
\begin{aligned} a(u,v) &= L(v)\cr &= \int_{\Omega} \nabla w \cdot \nabla v \,\mathrm{d}x\cr L(u,v) &= \int_{\Omega} 4\exp(-\beta^{2}(x^{2}+(y-R_{0})^{2})) v\,\mathrm{d}x \end{aligned}
# Define boundary condition
w_D = Constant(0) #w = 0 on boundaries
def boundary(x, on_boundary):
return on_boundary
bc = DirichletBC(V, w_D, boundary)
# Define load
beta = 8
R0 = 0.6
p = Expression('4*exp(-pow(beta, 2)*(pow(x[0], 2) + pow(x[1] - R0, 2)))', degree=1, beta=beta, R0=R0)
# Define variational problem
w = TrialFunction(V)
v = TestFunction(V)
a = dot(grad(w), grad(v))*dx
L = p*v*dx
# Solve
w = Function(V)
solve(a == L, w, bc)