Project Euler 199

Recently I was working on the Circle packing problem, which is a hard optimization problem. However, this Project Euler problem is not so much related to optimization problems, this is more of a geometric problem. I also had some fun doing this problem, plotting and generating an animation of the circles.

Statement

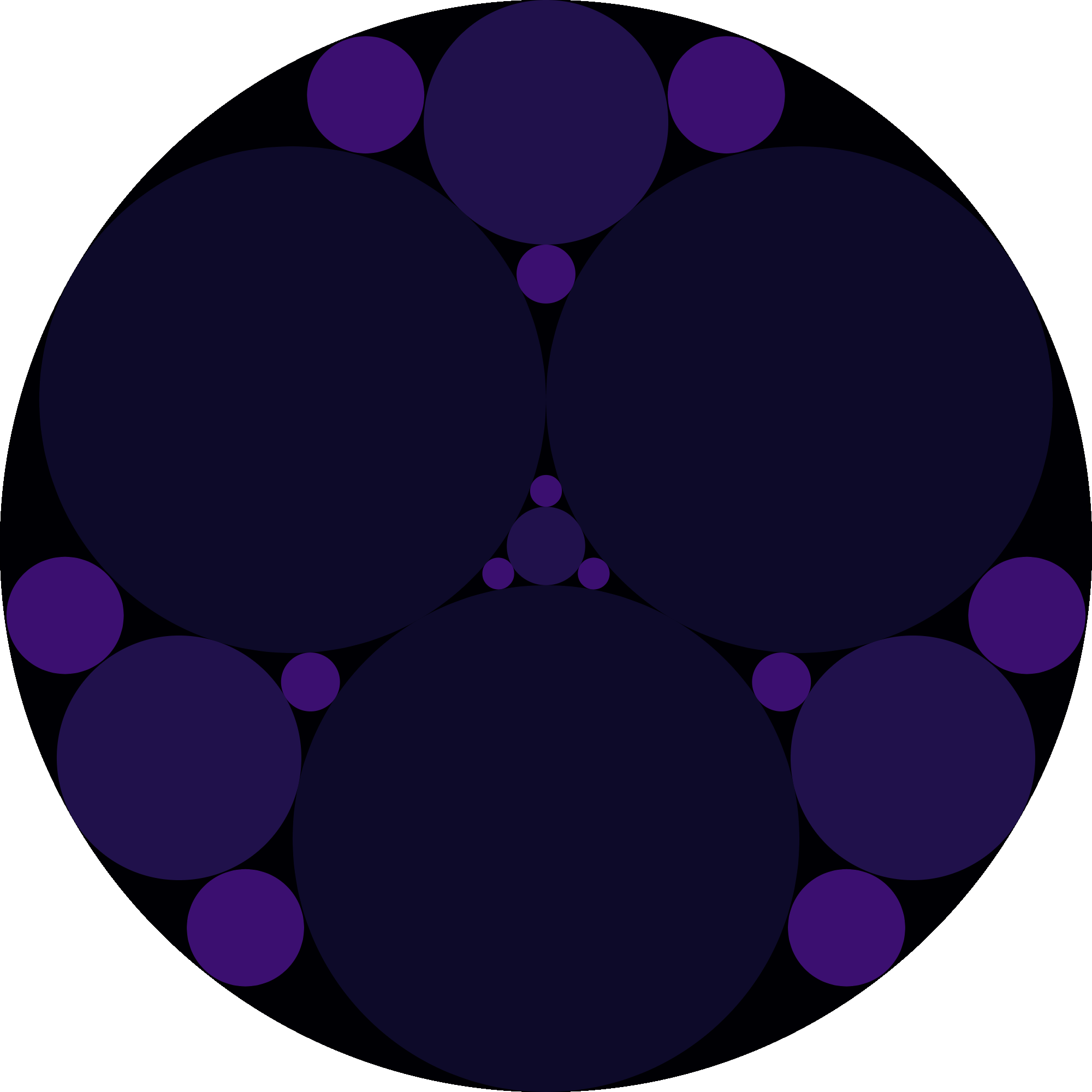
Three circles of equal radius are placed inside a larger circle such that each pair of circles is tangent to one another and the inner circles do not overlap. There are four uncovered “gaps” which are to be filled iteratively with more tangent circles.

At each iteration, a maximally sized circle is placed in each gap, which creates more gaps for the next iteration. After 3 iterations (pictured), there are $108$ gaps and the fraction of the area which is not covered by circles is $0.06790342$, rounded to eight decimal places.

What fraction of the area is not covered by circles after $10$ iterations? Give your answer rounded to eight decimal places using the format x.xxxxxxxx.

Solution

Calculating radius

Let’s see what happens with the first iteration:

It’s easy to see that the results are symmetric, in a $120^{\circ}$ fashion, and also includes a central circle that is also tangent to the three circles of iteration 0.

Let’s clarify this with a new iteration:

Let’s think of this as an iterative approach. If all the circles of the previous iteration are already determined, how can the circles of the new iteration be drawn?

Note that, a circle is always tangent to three other circles that were drawn in a previous iteration. Suppose, those circles are $A$, $B$, $C$ and the circle that is tangent to them is $H$, the circles in the next iteration are tangent to:

1. $A$, $C$, $H$
2. $B$, $C$, $H$
3. $A$, $B$, $H$

It means that, if you know what is the radius and center of a circle tangent to three other circles, you know how to place the circles for each iteration:

void solve(vector <vector <dd> > &radius){
    for(int level=1; level<=10; level++){
        vector <vector <dd> > new_radius;
        for(auto r_list: radius){
            dd r_A = r_list[0];
            dd r_B = r_list[1];
            dd r_C = r_list[2];
            dd r_H = gen_radius(r_A, r_B, r_C);
            new_radius.push_back({r_A, r_B, r_H});
            new_radius.push_back({r_A, r_C, r_H});
            new_radius.push_back({r_B, r_C, r_H});
        }
        radius = new_radius;
    }
}

In fact, it’s not needed to know the position of the circle, as you already know the circles are tangent. So, to save memory you can just store the radius of the circles in each iteration. Be cautelous, because the amount of circles increases expontenially in each iteration.

Now, let’s think how calculate the new radius knowing the radius of three circles to which it is tangent.

This problem is an special case of the called Problem of Apollonius, more specifically this could be solved using the Descartes’ theorem.

dd gen_radius(dd r_A, dd r_B, dd r_C){
    dd k = 1/r_A + 1/r_B + 1/r_C + 2*sqrt(1/(r_A*r_B) + 1/(r_B*r_C) + 1/(r_A*r_C));
    return 1/k;
}

Plotting circles

The problem is already solved, since it only needs the radius to compute the answer. However, if you want to see a nice animation about how the circles are being generated, you also need to calculate the coordinates.

The approach is really similar, just instead of storing the radius, store the circle.

void solve(vector <vector <_circle> > &circles){
    for(int level=2; level<=6; level++){
        // cout << "#############################\n";
        // cout << "LEVEL " << level << '\n';
        vector <vector <_circle> > new_circles;
        for(auto circles_list: circles){
            _circle new_circle = gen_circle(circles_list);
            cout << "Circle[{" << new_circle.second.first << ", " << new_circle.second.second << "}, " << new_circle.first << "],\n";
            new_circles.push_back({circles_list[0], circles_list[1], new_circle});
            new_circles.push_back({circles_list[0], circles_list[2], new_circle});
            new_circles.push_back({circles_list[1], circles_list[2], new_circle});
        }
        circles = new_circles;
    }
}

and to calculate the coordinates:

_point gen_coordinates(_circle c0, _circle c1, _circle c2, dd r){
    dd k0 = 1/c0.first;
    dd k1 = 1/c1.first;
    dd k2 = 1/c2.first;
    dd x0 = c0.second.first; dd y0 = c0.second.second;
    dd x1 = c1.second.first; dd y1 = c1.second.second;
    dd x2 = c2.second.first; dd y2 = c2.second.second;
    
    // (x0+iy0)*(x1+iy1) = x0x1 - y0y1 + i(x1y0 + x0y1)
    dd Sx = k0*k1*(x0*x1-y0*y1) + k1*k2*(x1*x2-y1*y2) + k0*k2*(x0*x2-y0*y2);
    dd Sy = k0*k1*(y0*x1+y1*x0) + k1*k2*(y1*x2+y2*x1) + k0*k2*(y0*x2+y2*x0);

    dd Cx = sqrt((sqrt(Sx*Sx+Sy*Sy)+Sx)/2);
    dd Cy = 0;
    if(Sy != 0) Cy = abs(Sy)/Sy*sqrt((sqrt(Sx*Sx+Sy*Sy)-Sx)/2);
    else if(Sx < 0) Cy = sqrt(-Sx);

    dd x_1 = (k0*x0 + k1*x1 + k2*x2 + 2*Cx)*r;
    dd y_1 = (k0*y0 + k1*y1 + k2*y2 + 2*Cy)*r;
    dd x_2 = (k0*x0 + k1*x1 + k2*x2 - 2*Cx)*r;
    dd y_2 = (k0*y0 + k1*y1 + k2*y2 - 2*Cy)*r;

    _circle c_1 = make_pair(r, make_pair(x_1, y_1));
    _circle c_2 = make_pair(r, make_pair(x_2, y_2));

    dd error1 = (check_tangency(c_1, c0) + check_tangency(c_1, c1) + check_tangency(c_1, c2));
    dd error2 = (check_tangency(c_2, c0) + check_tangency(c_2, c1) + check_tangency(c_2, c2));
    
    if(error1 < error2) return make_pair(x_1, y_1);
    else return make_pair(x_2, y_2);
}

To avoid precision errors, you need to check the tangency, but it’s not enough so you need to check the error in the two possible solutions.

P5.js

C++ is not a good language to make plots or animations, so I searched for other tools for this purpouse. I’ll use P5.js and I’ll port my C++ code to JS.

This is a plot in high resolution with $10$ iterations.

You can also make an animation using this tool.