I have so much fun with this problem maybe, because it's about euclidean geometry. I think the easiest part is to reach to some conclusions finding similarities and applying some geometry theorems, then the boring part is just the computation. Anyway, I think this will be a good excuse to draw some triangles.

Statement

Given an integer sided triangle $ABC$:

Let $I$ be the incenter of $ABC$.

Let $D$ be the intersection between the line $AI$ and the circumcircle of $ABC$ $(A \neq D)$.

We define $F(L)$ as the sum of $BC$ for the triangles $ABC$ that satisfy $AC = DI$ and $BC \leq L$.

For example, $F(15) = 45$ because the triangles $ABC$ with $(BC, AC, AB) = (6, 4, 5), (12, 8, 10), (12, 9, 7), (15, 9, 16)$ satisfy the conditions.

Find $F(10^{9})$.

Solution

As always, when you have a triangle and circumcircle, you can start thinking about cyclyc quadrilaterals, actually the point $D$ is a good point to start drawing a cyclic quadrilateral.

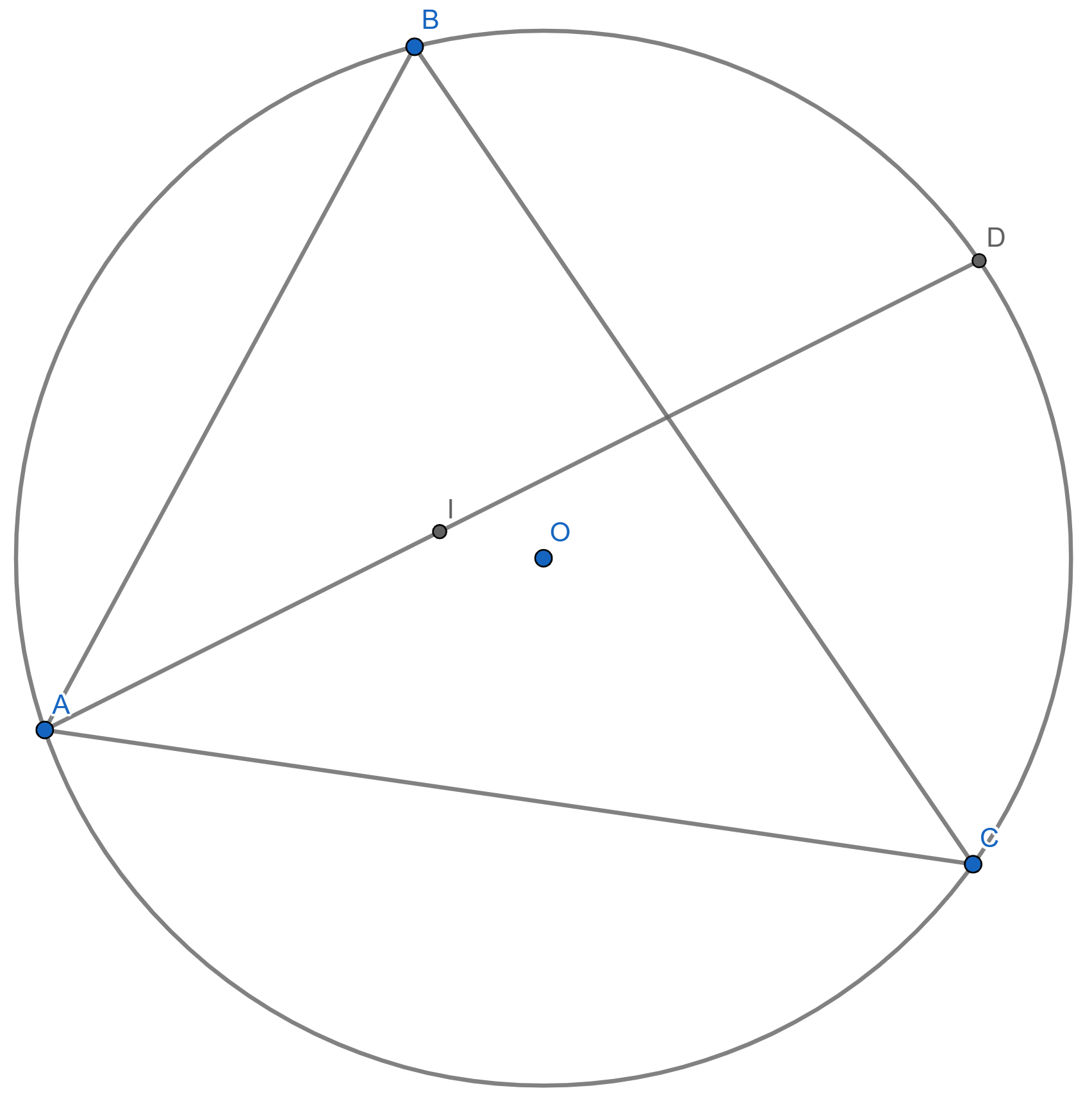
then, drawing the bisector for $\angle ACB$:

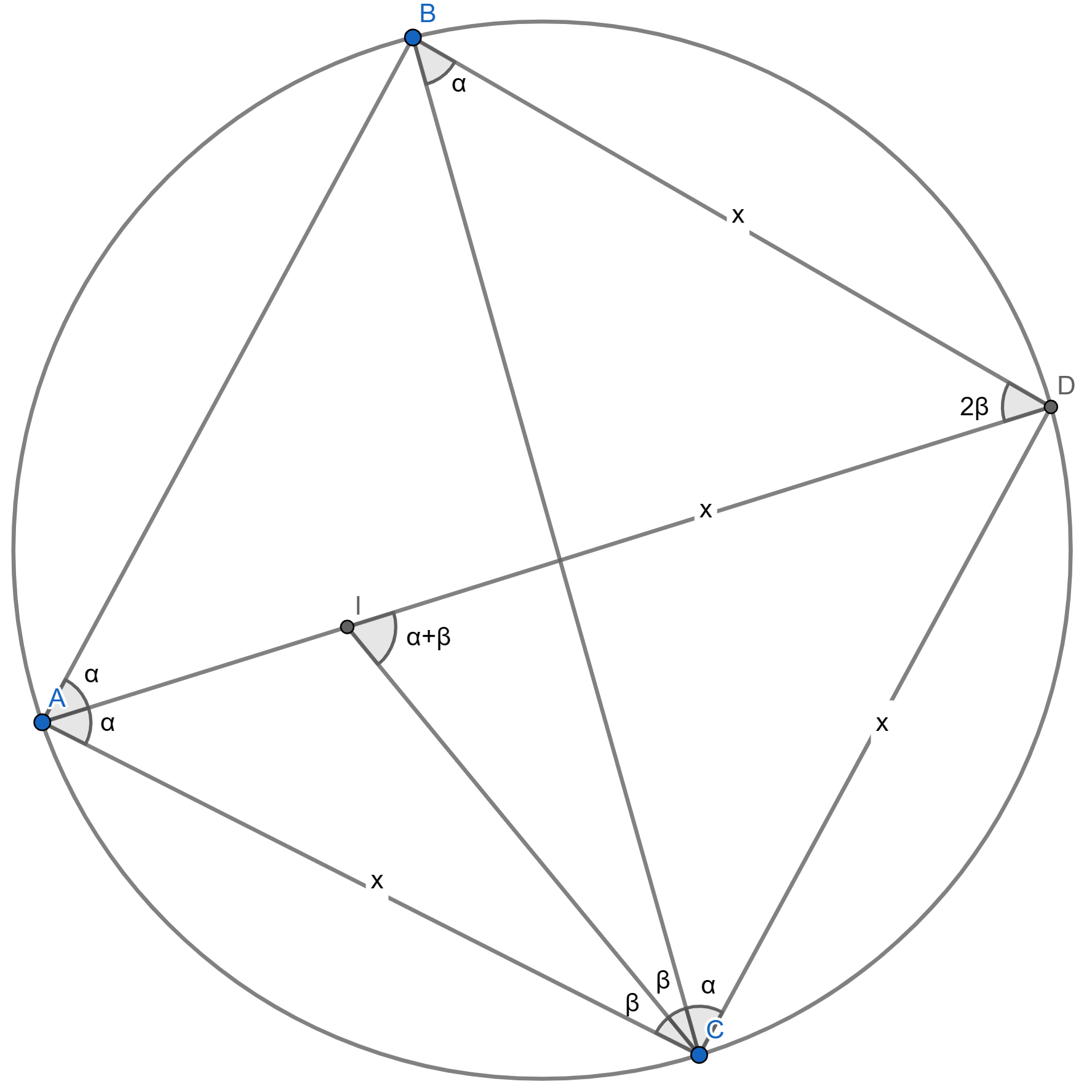
finally, just completing angles:

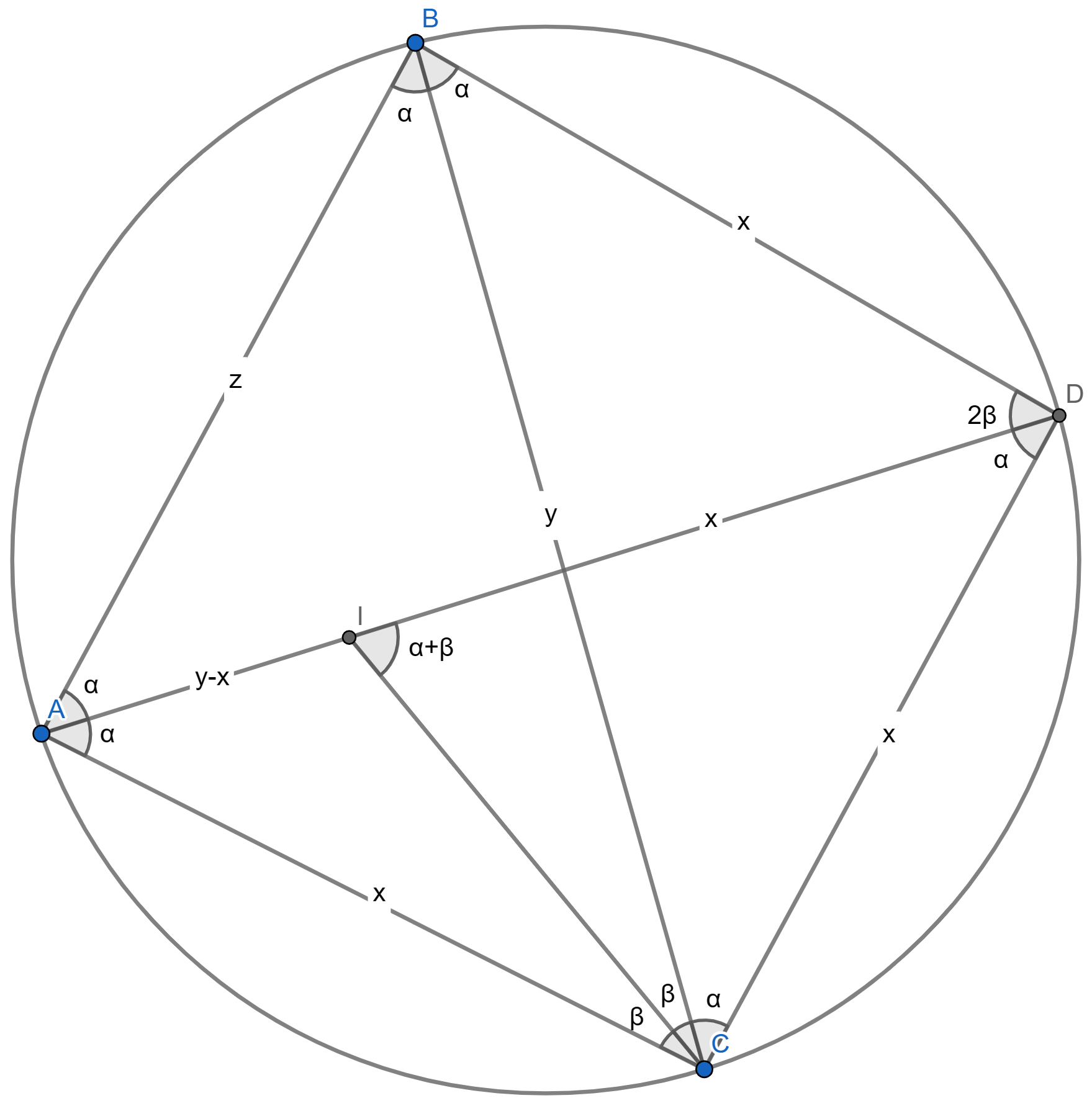
Applying Ptolemy's theorem:

$$xz + x^{2} = x(x+z) = y^{2}$$

Writing $x = \frac{m-z}{2}$:

$$m^{2}=2y^{2}+z^{2}$$

this problem is similar to generate pythagorean triplets, the only remaining step is to find the upper bound for $m$.

$$m < \sqrt{2}y+z\\ z < x+y\\ m < y(2+\sqrt{2})$$

Code

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
#define N 1000000000

int main() {
  int n;
  cin >> n;
  if (n == -1)
    n = N;
  n = min(n, N);
  ll ans = 0;
  for (int u = 1; 1LL * u * u < 3.42 * n; u++) {
    for (int v = 1; v < u && 1LL * u * v <= n; v++) {
      if (1LL * u * u + 1LL * v * v > 3.42 * n)
        break;
      if (__gcd(u, v) == 1 and (u % 2 == 0 or v % 2 == 0)) {
        ll m = 1LL * u * u + 1LL * v * v;
        ll double_a = 2LL * u * v;
        ll c = 1LL * u * u - 1LL * v * v;
        if (c > double_a)
          swap(c, double_a);
        if (double_a % 2 != 0) {
          m *= 2;
          c *= 2;
          double_a *= 2;
        }
        if (5 * c >= 3 * m or double_a > 2 * n)
          continue;
        int a = double_a / 2;
        int b = (m - c) / 2;
        int cnt = n / a;
        ans += (1LL * (cnt + 1) * cnt / 2) * a;
      }
    }
  }
  cout << ans << '\n';
  return 0;
}